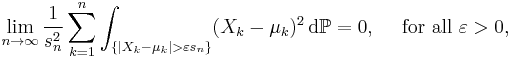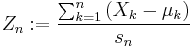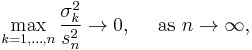Lindeberg's condition

In probability theory, Lindeberg's condition is a sufficient condition (and under certain conditions also a necessary condition) for the central limit theorem to hold for a sequence of independent random variables. Unlike the classical central limit theorem, which requires that the random variables in question to have finite mean and variance and be both independent and identically distributed, it only requires that they have finite mean and variance and be independent. It is named after the Finnish mathematician Jarl Waldemar Lindeberg.

Contents

Statement

Let 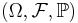(\Omega, \mathcal{F}, \mathbb{P}) be a probability space, and 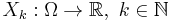X_k�: \Omega \to \mathbb{R},\,\, k \in \mathbb{N}, be independent random variables defined on that space. Assume the expected values 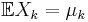\mathbb{E}X_k = \mu_k and variances 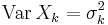\mathrm{Var}\,X_k = \sigma_k^2 exist and are finite. Also let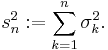 s_n^2�:= \sum_{k=1}^n \sigma_k^2 .

If this sequence of independent random variables 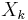X_k satisfies the Lindeberg's condition:

\lim_{n \to \infty} \frac{1}{s_n^2} \sum_{k=1}^n \int_{\{|X_k - \mu_k| > \varepsilon s_n\}} (X_k - \mu_k)^2 \,\mathrm{d}\mathbb{P} = 0, \quad \text{ for all } \varepsilon > 0,

(where the integral is a Lebesgue integral over the set 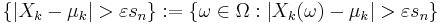\{|X_k - \mu_k| > \varepsilon s_n\}�:= \{\omega \in \Omega�: |X_k(\omega) - \mu_k| > \varepsilon s_n\}), then the central limit theorem holds, i.e. the random variables

Z_n�:= \frac{\sum_{k = 1}^n \left( X_k - \mu_k \right)}{s_n}

converges in distribution to a standard normal random variable as 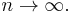n \to \infty.

Lindeberg's condition is sufficient, but not in general necessary (i.e. the inverse implication does not hold in general). However, if the sequence of independent random variables in question satisfies

\max_{k=1,\ldots,n} \frac{\sigma_k^2}{s_n^2} \to 0, \quad \text{ as } n \to \infty,

then Lindeberg's condition is both sufficient and necessary, i.e. it holds if and only if the result of central limit theorem holds.

Interpretation

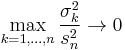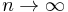Because, the Lindeberg condition implies \max_{k=1,\ldots,n}\frac{\sigma^2_k}{s_n^2} \to 0 as n \to \infty, it guarantees that the contribution of any individual random variable 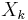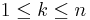X_k (1\leq k\leq n) to the variance 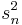s_n^2 is arbitrarily small, for sufficiently large values of n.

See also

References